 Existe relação entre matemática e música?
Existe relação entre matemática e música?
Decidimos construir esse tópico para mostrar como a matemática está relacionada com a música, afinal muita gente ignora o fato de que realmente existe matemática na música.
Talvez você não goste de matemática, mas não se preocupe, tentaremos explicar cada conceito de maneira simples, para que você perceba que nossa sensibilidade ao som está ligada à lógica de nosso cérebro. Isso é muito interessante, então deixe seus possíveis preconceitos de lado. Todo conhecimento é legal quando bem ensinado.
Antes de entrarmos no assunto de matemática na música, vamos relembrar alguns conceitos básicos.
A física na música
Ok, nos primeiros tópicos aqui do site, nós comentamos que o som é uma onda e que a frequência do som é o que define a nota musical.
Mas o que é uma frequência? É uma repetição com referência de tempo. Imagine, por exemplo, uma roda de bicicleta girando. Se essa roda completa uma volta em 1 segundo, dizemos que a frequência dessa roda é “uma volta por segundo”, ou “um Hertz”.
Hertz é apenas um nome dado para representar a unidade de frequência, e costuma ser abreviado para “Hz”. Se essa roda do nosso exemplo completasse 10 voltas em 1 segundo, sua frequência seria 10 Hertz (10 Hz).
Legal, mas o que isso tem a ver com o som? Oras, o som é uma onda, e essa onda oscila com uma certa frequência. Se uma onda sonora completar uma oscilação em 1 segundo, sua frequência será 1 Hz. Se ela completar 10 oscilações em 1 segundo, sua frequência será de 10 Hz.
Para cada frequência, temos um som diferente (uma nota diferente). A nota Lá, por exemplo, corresponde a uma frequência de 440 Hz.
A matemática na música
E onde entra a matemática nessa história? Observou-se que quando uma frequência é multiplicada por 2, a nota permanece a mesma. Por exemplo, a nota Lá (440 Hz) multiplicada por 2 = 880 Hz é também uma nota Lá, só que uma oitava acima, ou seja, mais agudo.
Se o objetivo fosse abaixar uma oitava, bastaria dividir por 2. Podemos concluir então que uma nota e sua respectiva oitava mantêm uma relação de ½.
Muito bem, antes de continuarmos, vamos voltar ao passado, para a Grécia Antiga. Naquela época, existiu um homem chamado Pitágoras que fez descobertas muito importantes para a matemática (e para a música).
Isso que acabamos de mostrar sobre oitavas ele descobriu “brincando” com uma corda esticada. Imagine uma corda esticada, presa nas suas extremidades. Quando tocamos essa corda, ela vibra (observe o desenho abaixo):

Pitágoras decidiu dividir essa corda em duas partes e tocou cada extremidade novamente. O som produzido era exatamente o mesmo, só que mais agudo (pois era a mesma nota uma oitava acima):

Pitágoras não parou por aí. Ele decidiu experimentar como ficaria o som se a corda fosse dividida em 3 partes:

Ele reparou que um novo som surgiu, diferente do anterior. Dessa vez, não era a mesma nota uma oitava acima, mas uma nota diferente, que precisava receber outro nome. Esse som, apesar de ser diferente, combinava bem com o som anterior, criando uma harmonia agradável ao ouvido, pois essas divisões até aqui mostradas possuem relações matemáticas 1/2 e 2/3 (nosso cérebro gosta de relações lógicas bem definidas).
Assim, ele continuou fazendo subdivisões e foi combinando os sons matematicamente criando escalas que, mais tarde, estimularam a criação de instrumentos musicais que pudessem reproduzir essas escalas.
O intervalo do trítono, por exemplo, foi obtido a partir da relação 32/45, uma relação complexa e inexata, fator que leva nosso cérebro a considerar esse som instável e tenso. Com o passar do tempo, as notas foram recebendo os nomes que conhecemos hoje.
Curiosamente, de um modo geral, o cérebro humano interpreta como “agradáveis” sons provenientes de valores pequenos no numerador e no denominador de uma fração, como as relações 2/3, 4/5, 8/5, etc. Já a fração 32/45 soa “desagradável”.
Apesar de não existir uma prova científica para justificar isso, o motivo pode ser a combinação de períodos, onde períodos muito desalinhados são mais difíceis de interpretar. Por exemplo, imagine um som que toca a cada dois segundos, juntamente com outro som que toca a cada 3 segundos (resultando em uma fração 2/3). O padrão resultante dessa combinação de dois ritmos poderia ser identificado rapidamente. Porém dois sons que tocassem nas proporções de 32 por 45 formariam um padrão rítmico mais difícil de decifrar. Se essa ideia não ficou muito clara, considere o seguinte:
Na prática, como já vimos, uma nota musical é formada por batidas tocadas rapidamente em sucessão (por exemplo: 220 batidas por segundo = 220 Hz).
Quando tocamos duas notas ao mesmo tempo, estamos comparando um som que bate x vezes por segundo com outro que bate y vezes por segundo, resultando em uma fração x/y.
Se a forma mais reduzida dessa fração resultar em números pequenos, significa que o padrão rítmico pode ser mais facilmente interpretado.
Em outras palavras, cada nota possui um ritmo associado, e o cérebro humano interpreta esses ritmos em um espectro de altura sonora (agudo ou grave). A sobreposição de duas notas, em sua essência física fundamental, é uma sobreposição rítmica. Se o ritmo resultante consiste em um padrão simples e identificável, a interpretação sonora é mais agradável.
A matemática das escalas musicais
Muitos povos e culturas criaram suas próprias escalas musicais. Um exemplo foi o povo chinês, que partiu da experiência de Pitágoras (utilizando cordas).
Eles tocaram a nota Dó em uma corda esticada e depois dividiram essa corda em 3 partes, como acabamos de mostrar. O resultado dessa divisão foi a nota Sol.
Ao observar que essas notas possuíam uma harmonia entre si, eles repetiram o procedimento a partir dessa nota Sol, dividindo novamente esse pedaço de corda em 3 partes, resultando na nota Ré.
Essa nota matinha uma harmonia agradável com a nota Sol e também com a nota Dó. Esse procedimento foi então repetido a partir da nota Ré, dando origem à nota Lá. Depois, partindo de Lá, chegou-se à nota Mi.
Quando eles repetiram esse procedimento de dividir em 3 partes a corda mais uma vez, dando origem à nota Si, houve um problema, pois a nota Si não soava muito bem quando tocada junto com a nota Dó (a primeira nota do experimento).
De fato, essas notas eram muito próximas uma da outra, o que causava um certo desconforto sonoro. Por isso, os chineses terminaram suas divisões obtendo as notas Dó, Sol, Ré, Lá e Mi, deixando a nota Si de lado.
Essas notas serviram de base para a música chinesa, formando uma escala de 5 notas (Pentatônica). Essa escala pentatônica, por ser agradável e consonante, representou muito bem a cultura oriental, que sempre foi pautada na harmonia e estabilidade.
Desde sua criação até os dias de hoje, a escala pentatônica representa uma ótima opção para melodias, como já comentamos no tópico “escala pentatônica”. Mas vamos voltar ao assunto de notas e frequências, afinal só mostramos até agora 5 notas da escala.
A matemática das 12 notas
A música ocidental, que trabalha com 12 notas, não descartou a nota Si como a cultura oriental havia feito.
Os ocidentais observaram que as notas Dó e Si eram próximas uma da outra e decidiram criar uma escala mais abrangente. Nessa escala, todas as notas deveriam ter a mesma distância umas das outras. E essa distância deveria ser o intervalo que havia entre Dó e Si (um semitom).
Ou seja, entre Dó e Ré, por exemplo, precisaria existir uma nota intermediária, pois a distância entre Dó e Ré (um tom) era maior que a distância entre Dó e Si (um semitom).
Por meio da análise de frequências, descobriu-se que multiplicando a frequência da nota Si pelo número 1,0595 chegava-se na frequência da nota Dó, observe:
- Frequência da nota Si: 246,9 Hz
- Frequência da nota Dó: 261,6 Hz
Multiplicando a frequência da nota Si por 1,0595 teremos:
- 246,9 x 1,0595 = 261,6 Hz (nota Dó)
Como nosso objetivo é manter essa mesma relação (distância) para as demais notas, vamos utilizar esse procedimento para descobrir qual será a nota que virá depois de Dó. Multiplicando a frequência da nota Dó por 1,0595:
- 261,6 x 1,0595 = 277,2 Hz (Nota Dó sustenido)
Repetindo o procedimento para ver o que vem depois de Dó sustenido:
- 277,2 x 1,0595 = 293,6 Hz (Nota Ré)
Observe que seguindo essa lógica, podemos formar toda a escala cromática! Ou seja, depois de multiplicar a frequência da nota Dó pelo número “1,0595” doze vezes, voltaremos à nota Dó.
Isso só é possível porque “1,0595” corresponde ao resultado da raiz:
![]()
Observe que essa raiz multiplicada por ela mesma 12 vezes é igual a 2:
![]()
E já vimos que uma nota multiplicada por 2 é ela mesma uma oitava acima.
Agora sim podemos ver claramente que esses números não saíram do acaso. O objetivo desde o início foi dividir uma escala em 12 partes iguais, de maneira que a última nota voltasse a ser a primeira.
Foi assim que surgiu a escala temperada, também chamada de cromática.
Encontrando as notas a partir das frequências
Tudo que discutimos ficará mais claro olhando para as notas em um piano:

Se considerarmos que o primeiro dó (mais a esquerda) possui frequência f, o segundo dó (uma oitava acima terá frequência 2f). Para chegar no próximo dó, teremos que pegar o dó 2f e multiplicar por 2 novamente, chegando no dó 4f. Repetindo o processo, o último dó desse piano será o dó 8f. Acompanhe a lógica:

Mas e quanto às frequências 3f, 5f, 6f e 7f, onde elas estão? Vamos descobrir. Primeiro vamos pensar sobre a frequência 3f. Ela está em algum lugar entre as frequências 2f e 4f. Sabemos que 1,5*2 = 3, portanto precisamos avançar uma quantidade k de semitons (onde cada semitom equivale a aproximadamente 1,0595, como já vimos) até resultar em 3f. Ou seja, (1,0595^k)*2f = 3f. Resolvendo para k, descobrimos que esse valor é 7, pois 1,0595^7 = 1,5 (aproximadamente).
Em outras palavras, precisamos avançar 7 semitons partindo de 2f até chegar na nota 3f. A conclusão é que a nota 3f é a nota sol:
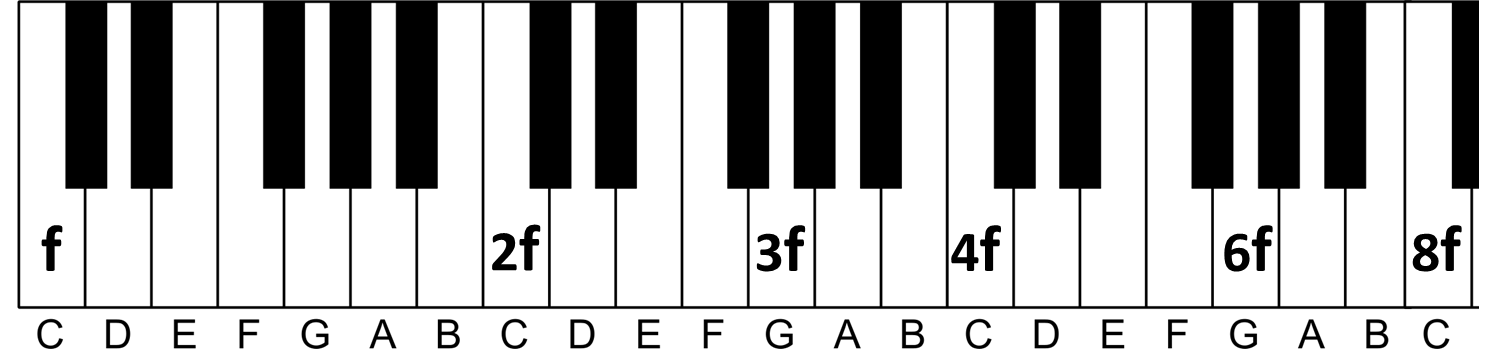
Repare que já podemos concluir automaticamente onde está a nota 6f, pois ela será uma oitava acima da 3f: 3f*2 = 6f. Por isso ela também já foi identificada acima.
Realizando o mesmo procedimento, podemos encontrar a nota 5f, que está no meio do caminho entre as frequências 4f e 6f:
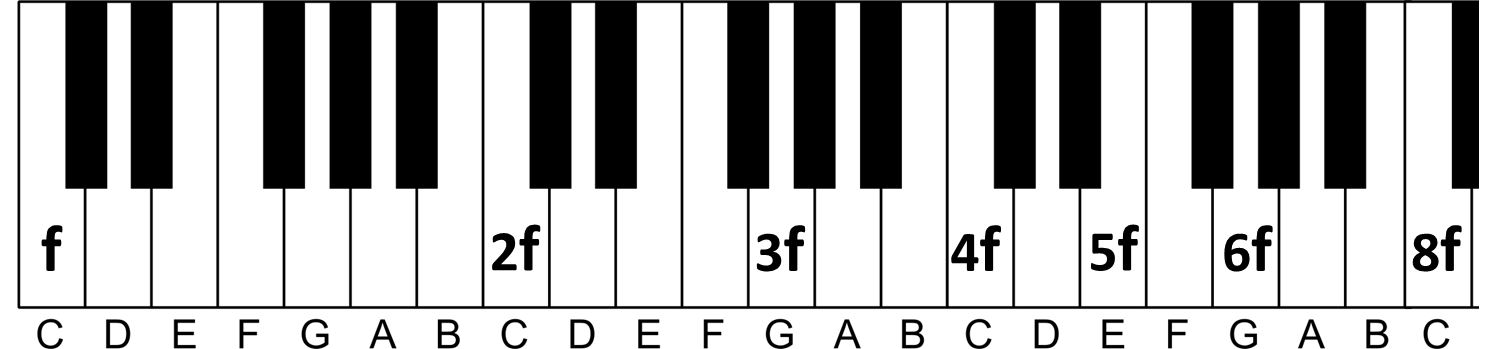
Agora podemos pensar de trás para a frente também para encontrar as frequências da primeira oitava. Até aqui sempre avançamos multiplicando por 2 para chegar nas notas mais agudas. Se quisermos encontrar as notas mais graves, basta fazer o processo inverso: dividir por 2.
Ou seja, a nota “E” (mi) denotada como 5f localizada uma oitava abaixo será (5/2)*f. E reduzindo mais uma oitava será (5/4)*f. O mesmo vale para a nota 3f:
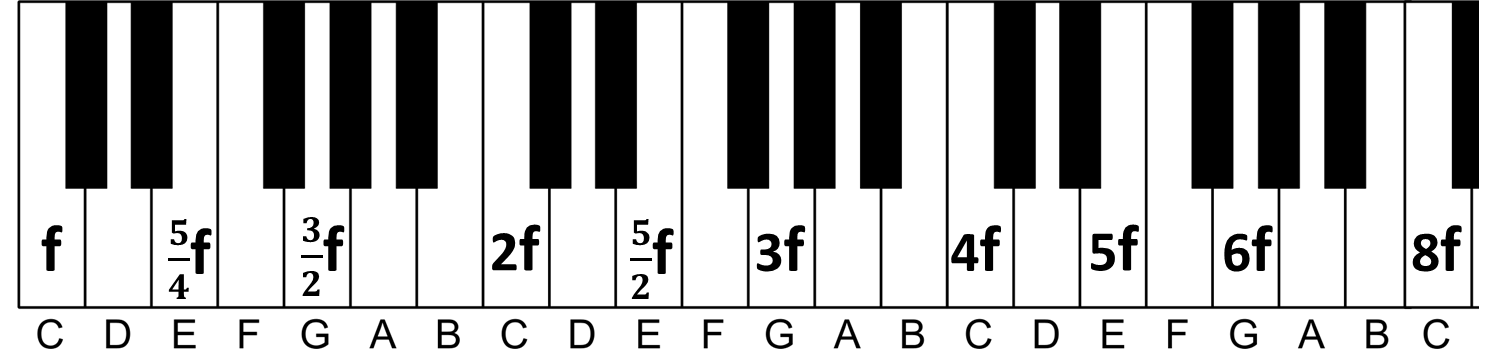
Agora tudo começa a ficar mais claro. As relações 5/4 e 3/2 que começamos falando nesse artigo quando mencionamos o experimento de Pitágoras estão se materializando em nosso piano.
Utilizando as mesmas técnicas abordadas até aqui, podemos estabelecer com precisão todas as frações da primeira oitava:
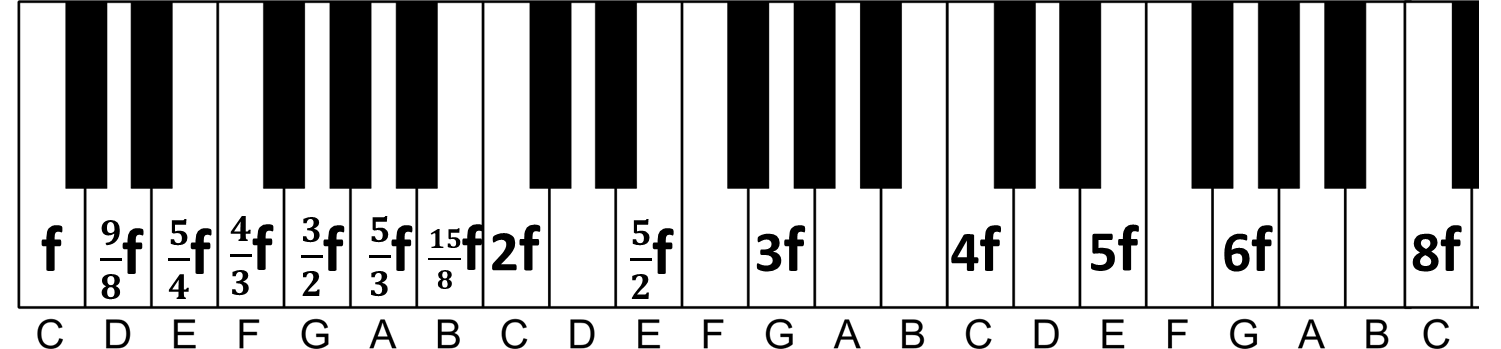
Para saber se duas notas tocadas ao mesmo tempo terão um som agradável, basta dividir suas frações e reduzir a expressão à sua forma mais básica. Se o resultado for um valor grande no denominador, a sensação será desagradável.
Exemplos:
O intervalo entre mi e si corresponde a uma quinta justa. Intervalos de quinta justa são bem agradáveis musicalmente falando. Podemos constatar isso matematicamente? Basta fazer (5/4) / (15/8) = 40/60 = 2/3. Fração simples (denominador pequeno), como esperado.
E o intervalo entre si e dó? Existe um choque sonoro entre si e dó (notas separadas por um semitom de distância não soam bem juntas). Vamos ver o que a matemática nos diz sobre esse intervalo: (15/8) / (2/1) = 15/16. Fração complexa, como esperado.
O logaritmo na música
Quem sabe um pouquinho de matemática reparou que, ao fazer os cálculos das frequências e raízes, nós trabalhamos intrinsicamente com o logaritmo de base 2.
Por isso, os construtores dos pianos colocaram a forma do gráfico de um logaritmo no corpo do piano, para fazer uma referência a essa descoberta matemática musical. Observe:
Exemplo de gráfico logarítmico:
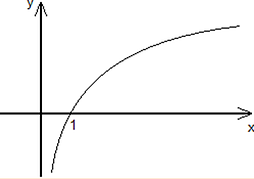
Corpo do piano:

Existem muitas outras explicações matemáticas para diversas questões da música, e para mostra-las aqui será necessário abordar assuntos mais avançados, como séries de Fourier. Uma série de Fourier pode ser utilizada para descrever o comportamento de uma onda na física. Basicamente, essa série é formada por um harmônico principal somado a outros harmônicos secundários. A equação pode ser descrita dessa forma:
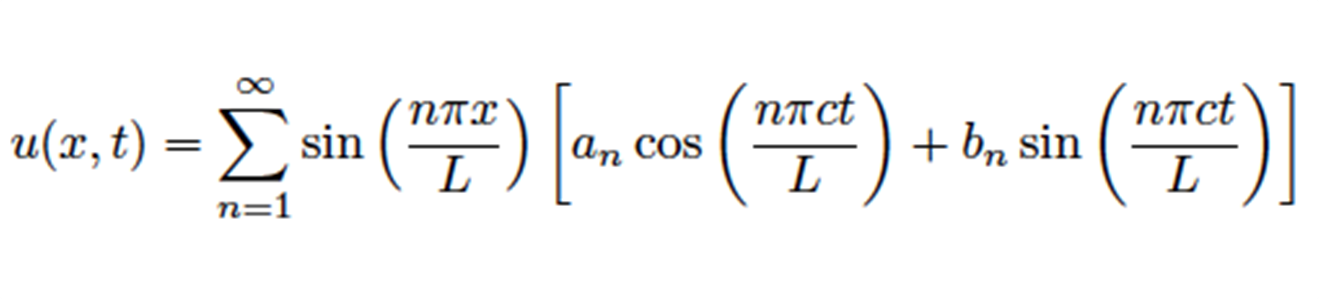
Quando uma corda vibra, o que ouvimos não é um som único puro, e sim uma superposição de vários sons, cujas frequências são todas múltiplas da frequência fundamental. A frequência fundamental é a principal, que contribui mais, e as demais frequências múltiplas são chamadas de harmônicos.
A quantidade de harmônicos confere “riqueza” ao som, deixando-o “mais preenchido”. O som de um diapasão, por exemplo, não possui os harmônicos mais altos, contendo basicamente só a frequência fundamental. Isso é ótimo para servir de referência (por esse motivo o diapasão costuma ser usado para afinar instrumentos), mas em contrapartida o diapasão possui um som pobre, sem muita beleza ou riqueza sonora.
A proporção com que os harmônicos são adicionados a uma frequência fundamental colabora na produção do timbre característico de cada instrumento. Por isso que a gaita de boca tem um som diferente da flauta, por exemplo.
E obviamente, diferentes materiais produzem diferentes harmônicos. Isso faz com que a produção de um instrumento de qualidade leve em conta cada característica de cada material, como o tipo de madeira usada no corpo de um violão.
Indo um pouco além, quando um músico pluga um instrumento por meio de um cabo até o amplificador, cada elemento nesse circuito pode acabar filtrando alguns harmônicos, o que reduz a qualidade do som. Por isso é muito importante investir não somente em um instrumento, mas em cada equipamento em particular.
O processo engenharia do som, que desenvolve dispositivos analógico-digitais para capturar as ondas sonoras e armazenar digitalmente busca sempre preservar ao máximo o formato da onda original. Edições em estúdio como remoção de ruído também utilizam esses conceitos, procurando identificar quais são os harmônicos que estão poluindo a onda original.
2.500 palavras depois…
Nosso objetivo foi mostrar como a música trabalha matematicamente e como as relações lógicas são compreendidas por nosso cérebro.
Obviamente, fizemos tudo aqui utilizando aproximações (números arredondados), pois uma análise mais apurada seria tediosa para a maioria dos leitores, bem como provas matemáticas e físicas mais rigorosas.
Não é necessário decorar tudo o que ensinamos nesse tópico, apenas guarde que a música não surgiu do nada, ela é resultado de uma organização numérica. A interpretação de tudo isso quem faz é o nosso cérebro.
A conclusão final é que, se você é músico, então você é (de uma forma ou de outra) matemático, pois as sensações de prazer que você sente ao ouvir música escondem cálculos subliminares.
Seu cérebro gosta de cálculos, ele é uma máquina de calcular! Quanto mais você praticar, estudar e conhecer música, mais essa faculdade vai se desenvolver. Provavelmente você vai começar a sentir prazer ao ouvir músicas que antes não lhe traziam grandes sentimentos.
Podemos comparar isso com um aluno de física do 1º semestre. Se ele ler um livro de física moderna, vai parecer grego pra ele, não vai lhe trazer prazer algum. Mas alguns anos depois, quando que ele já tiver alcançado uma base matemática sólida e se deparar com esse mesmo livro, talvez ele passe a amar esse assunto e queira dedicar sua vida a isso.
Voltar para: Descomplicando a Música